The Innovation Engine of Recombinatorial Space
The Explosive Dynamics of Combinatorial Growth From Ideas to Wealth
Combinatorics refers to the vast array of possible combinations or arrangements that can be generated by recombining a given set of elements, ideas, or components.
In mathematics, combinatorial growth represents exponential growth layered on top of exponential growth.
In systems theory, it is complexity building upon complexity.
I aim to show how combinatorics is a key driver of global growth and innovation, as each new idea or technology disproportionately expands the combinatorial possibility space leading to a self reinforcing cycle of growth and innovation.
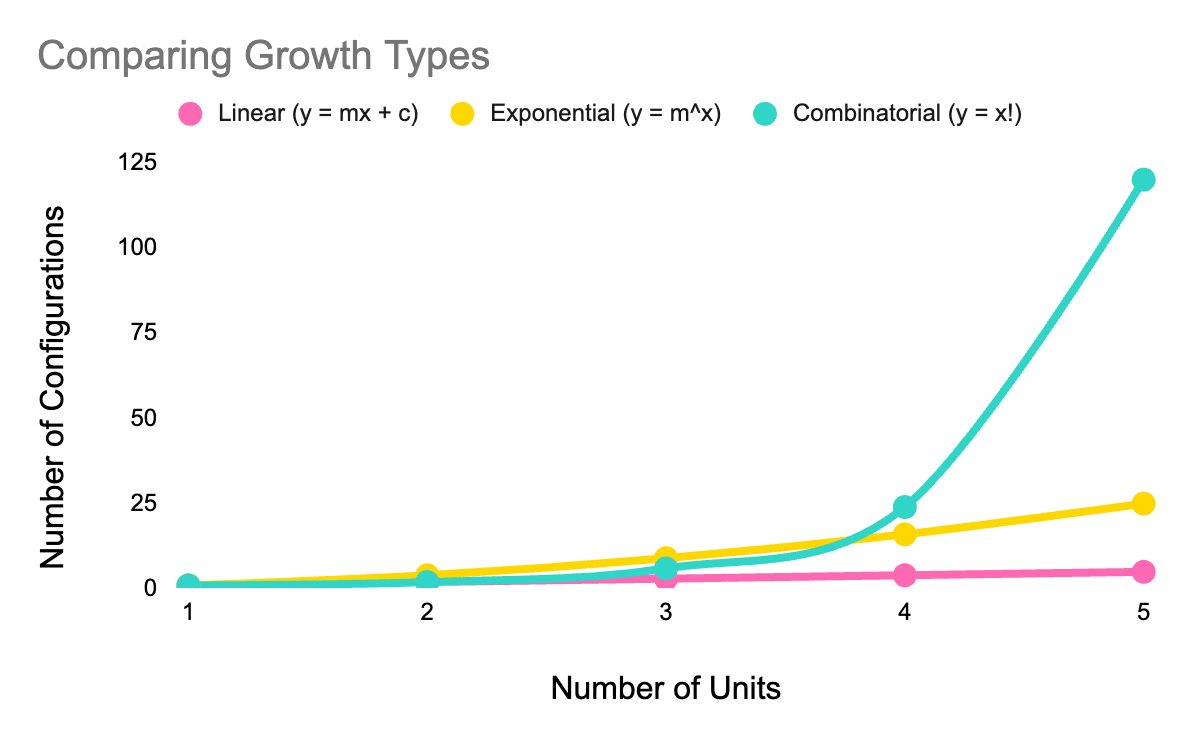
Comparing Different Types of Growth
As a simple illustration, consider the yellow circle one element (N).
A single element yields one possible combination.
Adding a second elements yields two combinations.
With three elements, there are six combinations.
Four elements results in twenty four combinations.
Five elements yields one hundred and twenty combinations.
The following graph illustrates how any system that follows combinatorics has a comparatively explosive growth acceleration as you add more elements. By only five elements, the linear growth function looks like a flat linen compared to the combinatorial growth function, which is already going parabolic.
Linear growth occurs at a constant rate, increasing by a fixed amount with each step or time unit. For example, if a business adds 10 new customers every month, after one month there are 10 new customers, after two months 20, and so forth. Graphically, this appears as a straight line.
Exponential growth increases at an accelerating rate, where the growth rate is proportional to the current value. For instance, if each customer tells two more customers, who in turn tell two more, the number doubles consistently. Graphically, exponential growth starts slowly but rapidly increases, resembling a J-shaped curve.
Combinatorial growth involves multiplying the number of combinations as new elements are added, resulting in a rapid escalation of possibilities. Due to the sheer multitude of combinations it propagates faster than standard exponential or linear functions.
Combinatorial growth is evident in businesses like social media platforms that leverage network effects. The value of such platforms grows not just by adding users linearly or exponentially, but combinatorially through the connections between users. As the number of users increases, the network’s value increases disproportionately from the potential user interactions.
The Paradox of Global Wealth
Combinatorial growth is the answer to the paradox of global wealth, which asks, how does global wealth continue to grow despite an increasing population? As new ideas and technologies emerge, they combine with existing ones, expanding the combinatorial possibilities disproportionately.
For example, Uber combined the existing technologies of mobile internet connectivity, GPS tracking and digital payment processing with the almost 300 million privately owned vehicles in the United States to create an entirely new product, unlocking $150 billion in value and growing the global economic pie.
As a more concrete illustration, if we frame the combinatorial growth space of innovation as physical land, it’s as if each new land discovery brings forth even more new land rising from the oceans.
So despite the omnipresent doomsayers, global wealth may actually be infinite.
Combinatorial Growth Both Expands and Compresses Time
Due to the limitations of physics, all available elements in a system cannot be experimentally combined simultaneously. Said another way, it takes time to rearrange physical objects or elements into different configurations. Time and distance and inextricably linked.
In classical mechanics, the relationship between distance and time is related through motion.
Distance = Speed x Time
In special relativity, space and time are interconnected in a four dimensional continuum known as spacetime. As objects approach the speed of light, time dilation and length contraction occurs, linking time and distance in a way that doesn’t exist in classical mechanics.
In general relativity, time and distance are influenced by gravitational fields. For near massive objects, time slows down (gravitational time dilation), and distances start to warp. For example, in cosmology light years (distance) are often used to describe astronomical scales of time since the speed of light is constant at that scale.
Since sifting through a vast recombinatorial space also takes a proportionately immense amount of time, it can stretch seconds into billions of years.
Consider the origins of complex life and the origins of human civilization.
Combinatorics was the Earth’s Early Prebiotic Innovation Engine, which took 4.5 billion years to recombine carbon with other simple molecules, evolving a primordial soup into the vast diversity of modern organic life.
Once complex life had evolved, the Combinatorial Innovation Engine of Early Civilization took only 2.6 million years for humans to dig up minerals and elements from the ground, apply fire and iterate from stone tools into a digital, spacefaring civilization.
Notice the time compression. Once an evolutionary search function hits on valuable recombination of elements, all the time it took finding the recombination gets rolled up into the new element, making it easier to replicate. Growth begets growth.
This is the Matthew effect of accumulated advantage, a natural phenomena so important and widespread it was even written down in the Bible.
“For to every one who has will more be given, and he will have abundance; but from him who has not, even what he has will be taken away.” Matthew 25:29, RSV.
“The Calling of Saint Matthew” by Caravaggio, 1599-1600
“Zero to One” by Peter Thiel is about creating groundbreaking businesses that move from “zero to one” by building something entirely new, rather than incrementally improving on what already exists. The book explores how to find unique opportunities, cultivate innovative thinking and create monopolies through technological breakthroughs, rather than competing in crowded markets.
Said another way, once a novel company or object is assembled, the time and work that was first required for construction gets compressed, making it easier to replicate. It’s harder to go from Zero to One then to One + N because of this compression phenomena.
Take modern humans for example. The spatial volume of the average human is about 62,000 cubic centimeters. However, when considering the required 4.5 billion years of time packed into the creation of those 62,000 cubic centimeters, unrolled we are enormous spatiotemporal beings. It’s no surprise that in terms of network power and depth of function, the human is considered the most complex thing in the known universe.
Remember that you are more ancient, towering and powerful than you think. After all, you have been traveling for 4.5 billion years in a wake of reassembled ancestral parts to be reading this text right now.