Fractal Geometry: Infinite Detail in Nature and Mathematics

The Map Is Not the Territory

Fractals are complex geometric shapes that can be split into parts, each of which is a reduced scale copy of the whole. This property is known as self-similarity. Fractals are found in both mathematical constructs and in natural phenomena, exhibiting patterns that repeat at different scales. They challenge traditional geometric notions because they can have infinite detail and can appear the same at different scales.

Fractal Surfaces

As an illustration of fractal geometry, let’s consider a non-obvious problem in measuring the coastline of Great Britan.

You could do it manually using a straight edge ruler and walk the whole coast taking measurements.

A faster alternative could be to use satellite imagery after choosing a specific unit of measurement. For example, 1 cm on the satellite map might equal 1 km in reality.

After gathering your measurements, you would sum the straight line distances between measurements after circumnavigating the whole island.

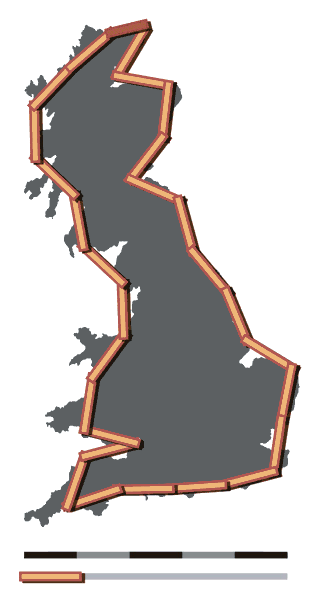
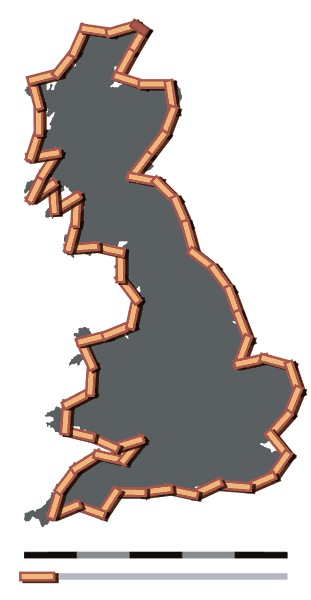
If you use a measurement unit of 100 km, then the length of the coastline is approximately 2,800 km (1,700 mi).

Now what if we change the size of our ruler?

Lets use units of 50 km instead of 100 km.

Now the total length becomes 3,400 km (2,100 mi). This is 600 km longer then the first measurement.

So how do we answer our original question, “how long is the coastline of Great Britan”?

This problem is called the coastline paradox. It was popularized by mathematician and grandfather of fractal geometry Benoit Mandelbrot. It highlights the counterintuitive observation that the length of a coastline can vary significantly depending on the method used to measure it.

This paradox arises from the fractal like properties of coastlines - as you zoom in to the coastline with a smaller and smaller ruler all the irregular shapes, such as bays, inlets and peninsulas, continue to increase the length.

Compare the following two pictures of the same coast line location at different scales.

The undulating coastline shape of the white cliffs of dover is not readily distinguishable from the same stretch viewed from satellite imagery.

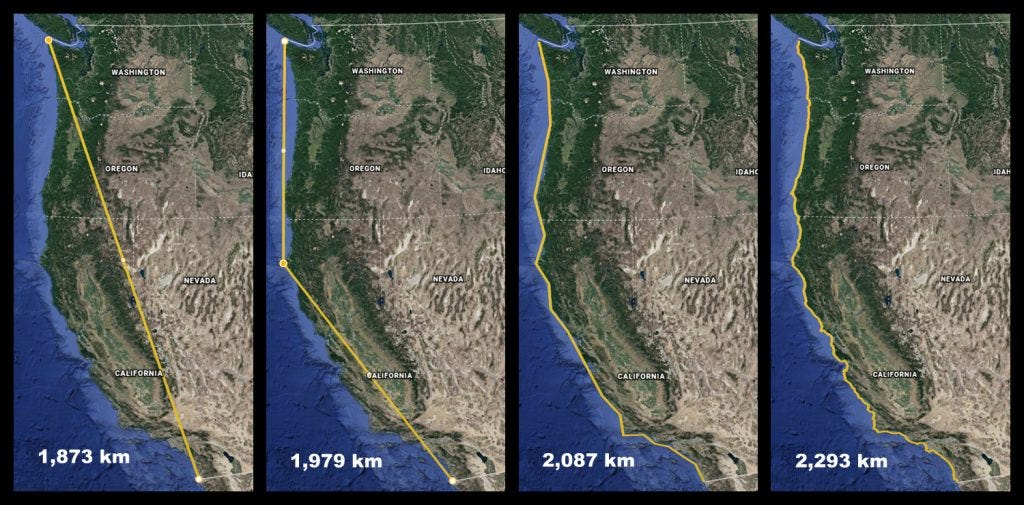
Here is a similar example, using the California coast, of how measurement scaling changes the measured.

Consider the following freshly sharpened knife edge.

It appears to have a smooth surface and looks straightforward to measure.

Using a scanning electron microscope, here’s the edge of the blade at 2000x magnification.

So how long is the blade?

What starts to become clear is that as we refine our detectors to measure smaller and smaller scales, the complexity we detect starts to increase.

Mandelbrot described this scaling phenomenon as the “roughness” or fractal characteristic of surfaces. Fractal mathematics describes how this complexity changes with scale.

The fractal principle is that the length approaches infinity as the measuring unit approaches zero.

Fractals in Nature

The classic Euclidean geometry we are taught in school deals only with smooth shapes. It is elegant, simple and practical. However, the natural world is not composed of straight lines, 45 degree angles and perfect circles. Instead, it appears the underlying architecture of the natural world is fractal.

Remember, fractals are geometric shapes that can be broken into smaller parts, with each part being a smaller scale version of the larger (fractal is actually the Latin term for broken). Let’s look at some examples.

A head of broccoli is made up of smaller heads of broccoli.

Each branch of a fern is composed of a smaller fern.

Each branch of a tree is a smaller version of the same tree.

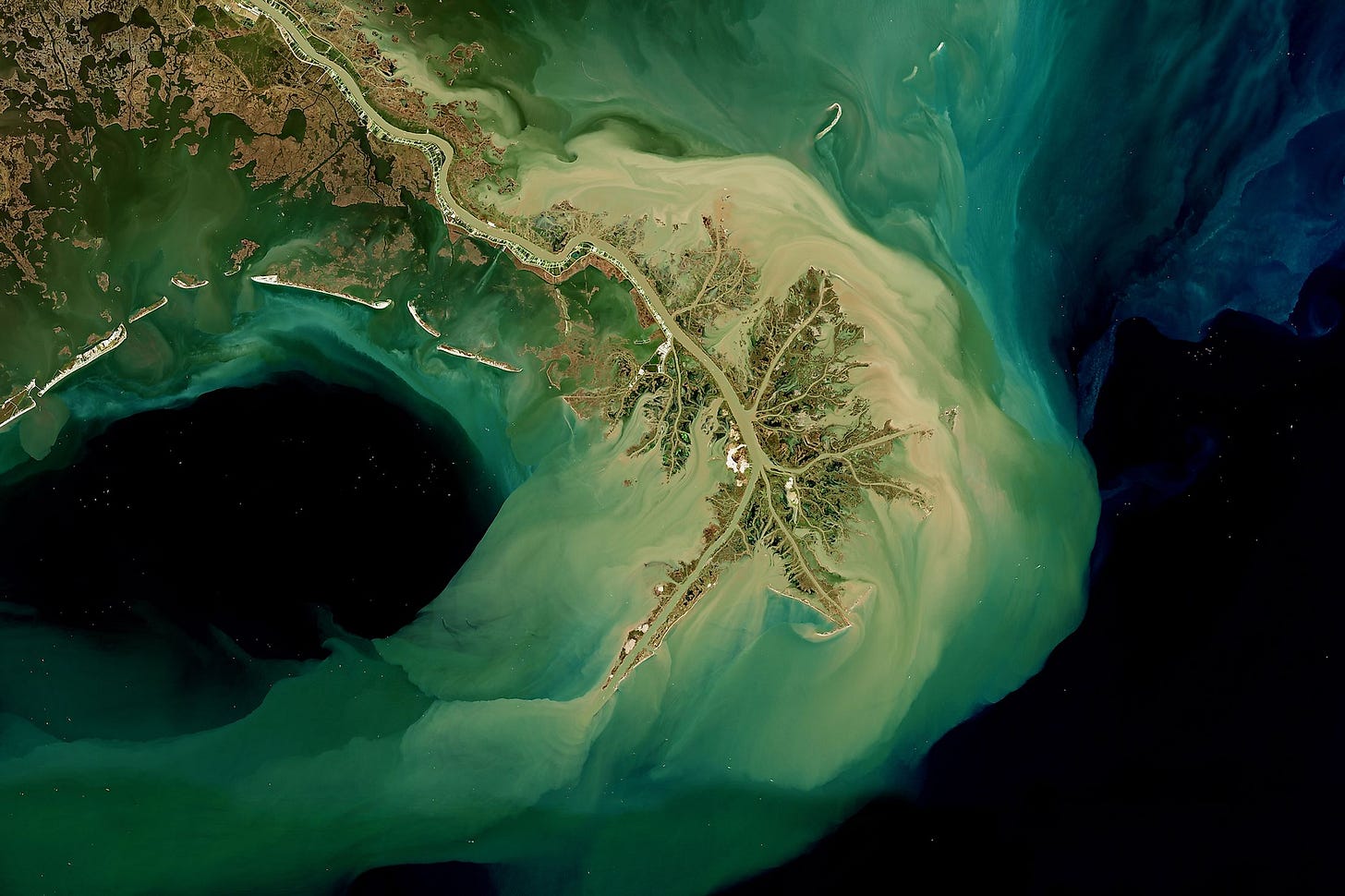
The fractal branching patterns of the Mississippi river delta.

The mighty mountain range of Patagonia consists of smaller, self similar individual mountains.

Cross Disciplinary Fractal Applications

Like all good mental models, the characteristics of fractal scaling and surface roughness can be widely applied.

It has been used to study patterns in human behaviors, such as the rhythms of daily activities and the timing of communications in social networks. These patterns often reveal self-similar structures over time, suggesting that human behavior may have underlying fractal characteristics. When you consider that we all run the same default human operating system, the seemingly cyclical nature of the geopolitical order and repeating self similarity of historical events starts to make sense through a fractal lens. As the ever insightful Mark Twain wrote, “history doesn't repeat itself, but it often rhymes.”

Financial markets have been analyzed using fractal geometry to understand the complex patterns of price movements and market trends. The concept of fractal markets hypothesizes that price movements are self-similar across different time scales, which can help in modeling market dynamics and in developing trading strategies. For example, the price action patterns that occur on a daily, monthly or annual chart can be self similar across scales of time. See Mandelbrot’s excellent book “The Misbehavior of Markets: A Fractal View of Financial Turbulence”

The structure and functioning of the human brain have been analyzed using fractal geometry, with researchers finding that neural activity often exhibits fractal patterns. This can be seen in the branching patterns of neurons and in the dynamics of brain activity, suggesting that the brain operates in a way that can be modeled by fractal processes.

The structure of social networks has been found to exhibit fractal characteristics, with patterns of connections that repeat at various scales. This insight can help in understanding the spread of information, the development of social norms, and the dynamics of group formation. It can also help us understand network effects, a business principle that suggests the value of a network increases as more people use it.

The layout and growth of cities often show fractal patterns, with self-similar structures evident in the distribution of housing, roads, and urban centers. Understanding these patterns can aid in more effective urban planning and in the design of sustainable living environments.

Consider the repeating patterns of suburban houses below.

In my view, some of the most important insights from fractals include:

• Recognizing that complex patterns often arise from simple rules repeated at different scales.

• Recognizing that these complex patterns can be highly artistic and aesthetic

• Understanding that solutions can have self-similar properties at different scales.

• Understanding how dynamic stability can emerge from iterative processes over time.

On a personal level, recognizing the fractal nature of human experiences and societal structures can lead to insights about personal growth, behavior patterns, and social dynamics. It suggests that individual actions and societal patterns are interlinked, each reflecting and influencing the other. It is butterfly effect propagating through a complex dynamic system.

After all, we are nothing more than nature examining itself.